Review of long steam turbine blade packet resonance

Interference Diagrams” also termed by some as “Safe Diagrams" are utilized for fully-coupled rotating blades. In Reference No. 1 resonance where harmonic of speed is equal to nodal diameters is reviewed, along with when difference in numbers of blades and vanes equal to number of diameters.

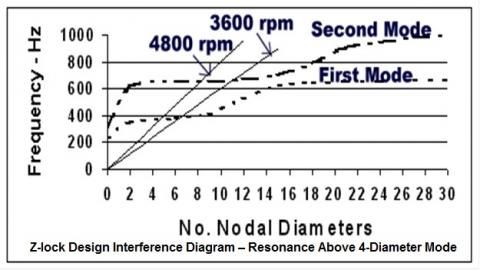
An example of nodal diameter “critical speeds” is shown above where there are 60 interlocked blades with a speed range of 3600 to 4800 rpm.

Nozzle passing frequency is not of much concern for modern designs utilize continuous shrouded blades, termed Z-lock or Z-notch, where there is beneficial friction damping at the shrouds. For long tapered, twisted blades there will be vibratory motion for each direction, axial and tangential giving first and second families of modes shown in the plot above.

Many other designs for long turbine blade are not fully connected (one packet) but are assembled into separate packets that could be resonant with even lower harmonics of speed. For these the tuned “Safe Diagram” theory is more likely to apply than for short blades as described in the author’s previous article. Each packet of long blades could have individual frequencies very close to each other, just as assumed with models for finite element analyses. Tuned packets result in coupled modes where patterns produce diametral nodal lines with adjacent packets out-of-phase with each other. With 24 packets the highest in-phase mode would have 12 diameters as shown in the figure below for 120 blades, 24 tuned packets with five nearly identical last stage blades per packet.

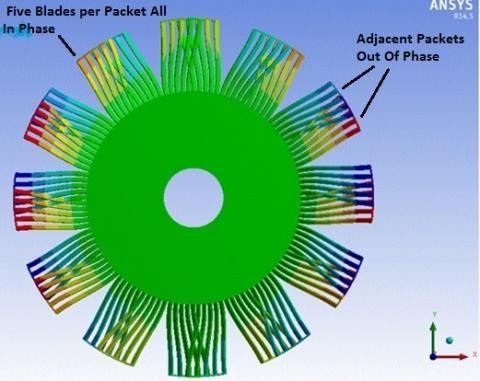
12 Diameter Mode Shape: 12 packets In-Phase and 12 Packets Out-of Phase

Lower harmonic excitation can arise from non-uniformity of upstream nozzles as well as potential flow of non-uniform 90-degree exhaust casings. Can the 24-packet assembly respond for resonance with five times operating speed of the fundamental In-Phase mode? There would be response for this example as five is less than 24/2 = 12.

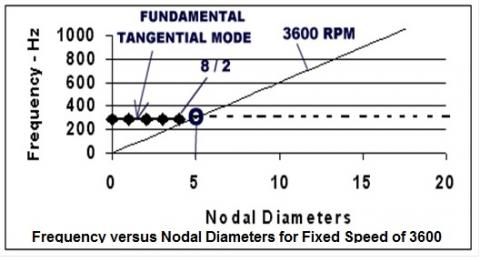
If this design has 10 or more packets it could respond with fairly high response at 5X. With 24 packets five times speed would excite the 5-diameter mode. But by changing to only  8 packets some claim it would not respond if it was tuned; i.e. the point 8 over 2 = 4 shown in the figure above is less than 5 times running speed. The five diameter mode would not exist for eight tuned packets. Due to phase cancellation five times speed also would not excite a 4-diameter mode if its frequency was at five time speed. Note that nodal diameter frequencies are close together in the figure above. In Reference 4 the authors Wagner and Griffin give an equation to use to check for other cases of tuned packet response where they say for a mode wirh "m" diameters:

It was shown in Part I that the condition required for an N group bladed disk to respond to an excitation harmonic h while constrained to mode harmonic m is given by h = jN ± m

where j = 0, 1, 2, . . . , with the further condition that h cannot be negative, and that negative values of m need not be considered.

Thus for 120 blades with eight packets, a 3-diameter mode has response when at resonance with five times speed as: 5 = 8 packets – 3.

See Table 2 highlighted in red below showing positive participation factor.

For certain numbers of blades and packet selections even tuned assemblies will respond. With a change to 112 total blades and using seven packets with 16 blades there would be phase cancellation if the 3-diameter mode was resonant with 5 times speed. However the possibility of mistuned packets should also be considered, not only from design and manufacturing differences, but from changes during operation such as from erosion/corrosion. Using many more blades per packets than five or six is usually much better for phase cancellation. An example of experimental results for a case with 12 packets, resonant with 3X is shown in Figure 10 of Reference 5.

Let us again review a design with 120 rotating blades, but with mistuned packets, resonant with five times speed. Recommending a change from 24 packets to 8 packets will reduce the resonant response factor at 5X speed from 0.93 to 0.47 as shown in the table below. This may not be safe enough, especially if the stage is a transition stage with wet steam and corrodants in the steam. The optimum would be five packets of blades; the resonant response factor would be near zero for the fundamental mode. This is called the “long arc” or “harmonic shrouding” method of selecting blade packets for back-end stages. (Reference 6). Using Weaver & Prohl equations with excitation at the 5’Th harmonic:

Table: Resonant Response Variation with Packet Changes

              120 Blades : Resonance Of Fundamental IN-Phase Mode With 5 X Speed

Number Of Blades Per Packet

 Packet Resonant Response Factor

                       4

                    0.96

                       5

                    0.93

                      15

                    0.47

                      24

                    0.00

It usually turns out where shrouds are attached with peened-on tangs that as many blades as possible should be used instead of only five or six per packet often found in practice. (Some older designs are welded into groups). However all designs should be checked with Weaver and Prohl equations for fundamental mode response. For some stages with very low “Goodman Factors” checking the next highest packet mode where half the blades vibrate out-of-phase with the other blades may also be needed as explained in References 1 and 4.

This review is for fundamental modes with vibration in tangential direction; similar analysis applies to fundamental axial direction in-phase modes. Again for long tapered, twisted blades there will be vibratory motion for each direction for the axial and tangential mode families. Failure analysis of high cycle fatigue of blades assembled into packets should review potential resonance, reduction in strength of excitation sources, and the benefit of change to an optimum number of blades per packet. In addition correct operating conditions and steam purity must be reviewed for root cause failure analysis.

References:

 1. Kushner, F., 1979, “Disc Vibration - Rotating Blade and Stationary Vane Interaction,” ASME Paper No. 79-Det-83: 1980 ASME Transactions, Journal of Mechanical Design, 102, pp. 579-584.

2. Weaver, F. L., and Prohl, M. A., 1958, “High Frequency Vibration of Steam Turbine Buckets,” Trans. ASME, Vol. 78, pp. 181-189, 1958.

3. Kushner, F., 2004, "Rotating Component Modal Analysis and Resonance Avoidance Recommendations," Tutorial, Proceedings of the 33rd Turbomachinery Symposium, Turbomachinery Laboratory, Texas A&M University, College Station, TX.

4. Wagner, L. F. and Griffin, J. H., 1996, “Forced Harmonic Response of Grouped Blade Systems: Part II—Application,” ASME Journal of Engineering for Gas Turbines and Power, 118, pp. 137-145.

5. Sanvito, M., Pesatori, E., Bachschmid, N., Chatterton, S., 2012, “Analysis of LP Steam Turbine Blade Vibrations: Experimental Results and Numerical Simulations”; 10th International Conference on Vibrations in Rotating Machinery, IMech, pp 189 – 197.

6. Ortolano, R.J., La Rosa J.A., and Welch W.P., 1981, "Long Arc Shrouding - A Reliability Improvement for Untuned Steam Turbine Blading," ASME J. Eng. Gas Turbines Power 103(3), pp. 522-527.

frank_kushnner (at) comcast.net