Compressor performance and thermodynamics
Impact of Thermodynamic Property Accuracy on Compressor Performance
By Mark Sandberg
Figure 1: Multi-Section Compressor on Factory Test Stand

Knowledge of centrifugal compressor thermodynamic performance is critical to initial acceptance and, once installed, periodic or continuous health monitoring to ensure that the operation is consistent with the original design expectations. The accurate determination of this performance is dependent upon a number of factors. These include uncertainties associated with measured parameters of pressures and temperatures, composition of gas mixtures, and the calculated thermodynamic properties that are derived from these parameter measurements.
Industry standards, ASME PTC 10 and the ISO equivalent, ISO 5389, define some fundamental compressor performance measures that are universally accepted to describe their thermodynamic behavior. The polytropic work (or poly-tropic head) represents the useful work that is applied to the gas to raise its pressure from suction to discharge conditions. It is expressed by the following equation based upon the work of Schultz and the definition of a polytropic process for an ideal gas:
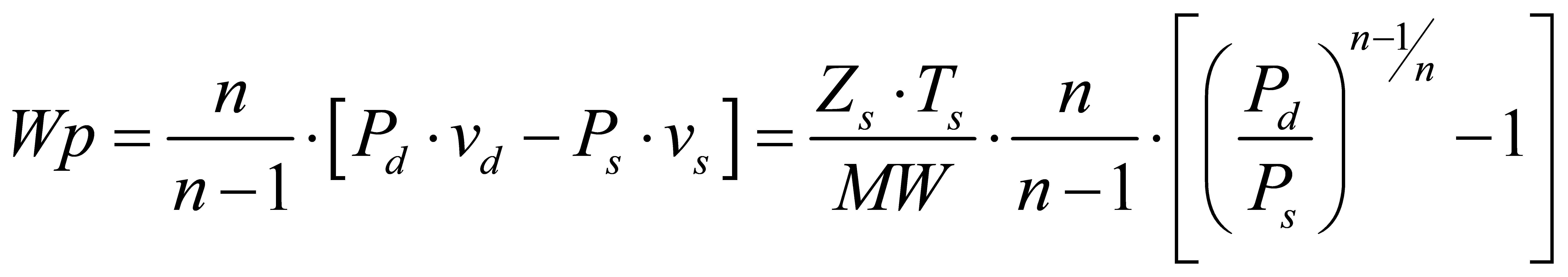
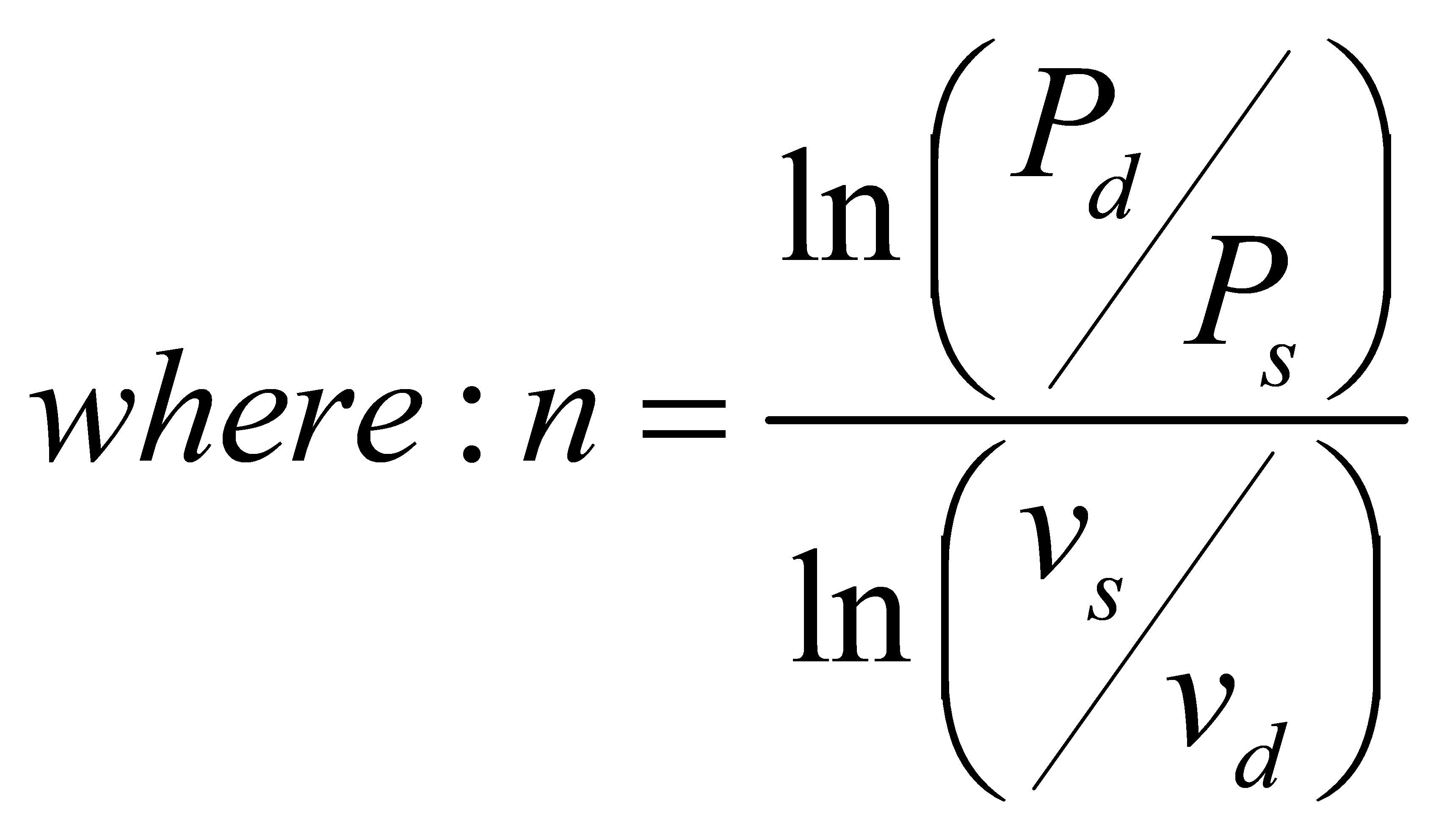
This equation shows that the polytropic work (Wp) is only dependent upon the compressor suction and discharge values of pressure (P), temperature (T), specific volume (v), and the gas molecular weight (MW). The average polytropic exponent, n, included in these relations is also derived from these parameters. These properties are all available from some equations of state for the gas. However, the polytropic work (useful work) does not represent the total amount of work required by the compression process.
An additional amount of work known as the lost work is consumed to raise the gas from suction to discharge pressure. Lost work manifests itself as an increase in the thermodynamic property of entropy of the gas or gas mixture and an additional increase in temperature above what would be expected for only the useful work also known as an isentropic process. The combined useful and lost work result in an increase in the total energy of the gas, also referred to as the increase in the thermodynamic property of enthalpy. Thus, the ratio of the polytropic work to the total enthalpy increase of the gas defines the polytropic efficiency of the compression process.
All thermodynamic properties needed to calculate compressor performance can be derived from three progressively complex thermodynamic models. The simplest, a perfect gas, requires only the pressure, temperature and gas molecular weight to obtain the specific volume, or its reciprocal the gas density, and the polytropic work. The enthalpy and entropy are calculated using constant values of the specific heat for a given gas or gas mixture and the temperature differential from suction to discharge of the compressor.
As the gas behavior becomes more complex, the perfect gas model needs to be modified with the addition of the specific heats becoming a func-tion of the temperature. This results in a more involved functional relationship with temperature needed to calculate the enthalpies and entropies required. An added parameter, the gas compressibility factor Z, is also introduced but its value is held at unity with the specific volume derived being equal to that of the perfect gas relation.
The most complex thermodynamic model is the real gas model. There is a compressibility factor, Z, which is a function of both the pressure and temperature with a more complex calculation of the specific volume than the simpler models. Additionally, the specific heat parameters are also functions of both pressure and temperature, resulting in more difficult relations needed to calculate the resulting enthalpies and entropies.
Figure 2: Pressure-Enthalpy Diagram for Methane
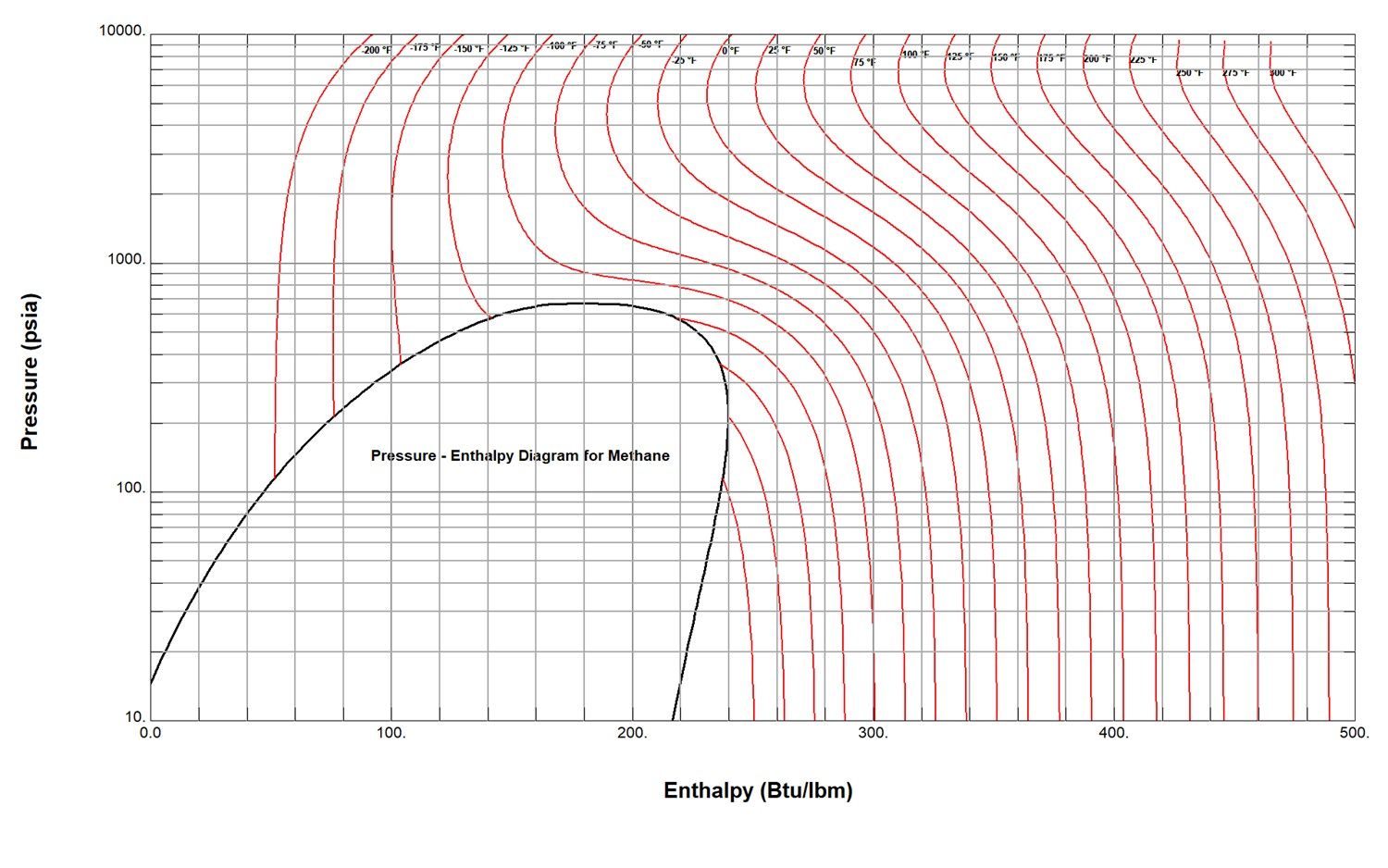
A more visual comparison of the enthalpy behavior of a gas is available through the examination of a pressure versus enthalpy diagram for a substance. Figure 2 is such a diagram for pure methane. The red isotherms which display near vertical linear characteristics at low pressures and higher temperature values reflect ideal gas behavior. These isotherms demonstrate increasing curvature at higher pressures which indicates progressive real gas performance with influences of both temperature and pressure present. A perfect gas would display consistent deviations in enthalpy for equal deviations in temperature and this is approximately noted at the lowest pressure levels and moderate temperatures where the changes in specific heat with temperature are minimal.
Although perfect and ideal gas relations may be limited in their application to given pressure and temperature conditions, it is assumed that real gas relations are valid across a broad range of con-ditions including ideal gas conditions. The corresponding values of specific volume (compressibility factor), enthalpy and entropy are more generally applicable when compared to the sim-pler perfect and ideal gas thermodynamic models.
REAL GAS EQUATIONS OF STATE
A substantial number of equations of state (EOS) have been developed over the past century to describe the thermodynamic behavior of substances, including several particularly focused on the vapor phase. The ideal gas EOS is generally applicable to simple molecules at low pressures due to the limited interactions between the particles that are relatively sparsely distributed in relation to one another within an arbitrary volume. As pressures increase and the gas molecules become more populated within a fixed volume and complex in both geometry and electro-magnetic polarity, the resulting attractive and repul-sive forces impact the ability of the ideal gas EOS to accurately describe the thermodynamic behavior. Under these more challenging conditions, more complicated relations are needed to ade-quately predict the gas properties. Although generally expressed as a single compressibility factor, Z, applied to the ideal gas EOS, the equations behind the determination of the compressibility factor and other, associated properties can be quite complicated.
Six selected real gas equations of state will be included in the following comparisons due to their typical application with gas compression. They can be separated into the four major categories provided below along with some historical perspective:
1. Cubic Equations of State
The van der Waals EOS was one of the first proposed beyond the ideal gas EOS. Subsequent improvements to the van der Waals equation included the Redlich-Kwong (R-K), Soave, and the Peng-Robinson (P-R) EOSs, including a number of others. These became known as cubic equations of state due to the fact that they expressed the pressure in terms of a cubic relationship to the specific volume. Alternatively, the compressibility factor could also be expressed as a third-degree polynomial which could be solved explicitly. The R-K EOS included only two com-ponent specific parameters that were derived from the critical pressure and temperature of that component. The Soave and P-R EOSs included a third parameter that was named the Pitzer acentric factor which was experimentally determined and further accounted for molecular polarity and non-sphericity.
Observations demonstrated that the cubic equations of state provided estimations of the compressibility factor that were offset from experimental values across a wide range of pressure and temperature conditions. Peneloux initially proposed a volume-translation method for the Soave equation of state that addressed this shift. Several other volume translation methods have been pro-posed for cubic equations of state. The method proposed by Jhaveri and Youngren has been included here as applied to the P-R EOS and is designated as the VTPR EOS for comparison.
2. Virial Type Equations of State
A more complex equation of state was proposed by Beattie-Bridgeman that included higher order specific volume terms and was considered to be more accurate than the cubic equations of state at the time. Benedict, Webb and Rubin proposed an expansion of this relation and Starling added additional terms which resulted in the BWRS EOS with a total of eleven empirically derived constants for each gas component, three more than its predecessor. Although significantly more complicated than the cubic equations of state, these thermodynamic models claim increased accuracy.
More recent variations of this class of equations of state offer additional accuracy but include more than thirty empirically derived constants for indi-vidual gas components. The actual Virial Equation of State is a similar power series expansion with constants that are a function of temperature.
3. Corresponding States Principle Equations of StateThe Corresponding States Principle (CSP) is based upon the fact that different gases demon-strate similar thermodynamic characteristics when the pressure and temperature are normalized with their respective critical values. A number of alternate versions of various equations of state have also been developed using the normalized (reduced) pressure and temperature as variables.
Probably the most accurate of these was devel-oped by Lee and Kesler and later modified by Plöcker, known as the Lee-Kesler-Plöcker (LKP) EOS. It is based upon the BWRS EOS using “simple” fluid and “reference” fluids combined with the Pitzer acentric factor for the selected gas or gas mixture.
While not being included in this comparison, there are some notable generalized CSP equations of state that can be utilized with reasonable expected accuracies. A generalized equation of state is one that does not require a detailed gas mixture composition but rather simply a presumed hydrocarbon mixture molecular weight and mole fraction compositions of the sour/acid gas components of nitrogen, carbon dioxide and hydrogen sulfide. The hydrocarbon mixture molecular weight is used to calculate values of pseudo-reduced values of pressure and temperature. Two of the more accurate generalized CSP equations of state are those developed by Dranchuk-Purvis-Robinson and Dranchuk-Abou-Kassem. These are typically used in oil and gas production applications where detailed gas mixture compositions are not known or variations are expected.
4. Helmholtz Energy Equations of State
A recent and stated highly accurate new form of an equation of state is the one developed by the Groupe Européen de Recherches Gazières (GERG). It is based upon the Helmholtz free energy which is a function of the internal energy and entropy of a substance and one of the fundamental thermodynamic energy functions. Similar to the virial family of equations of state, it is dependent upon a large number of empirically obtained constants for each of the included gas components.
Figure 3: Equation of State Comparison for Typical Natural Gas.
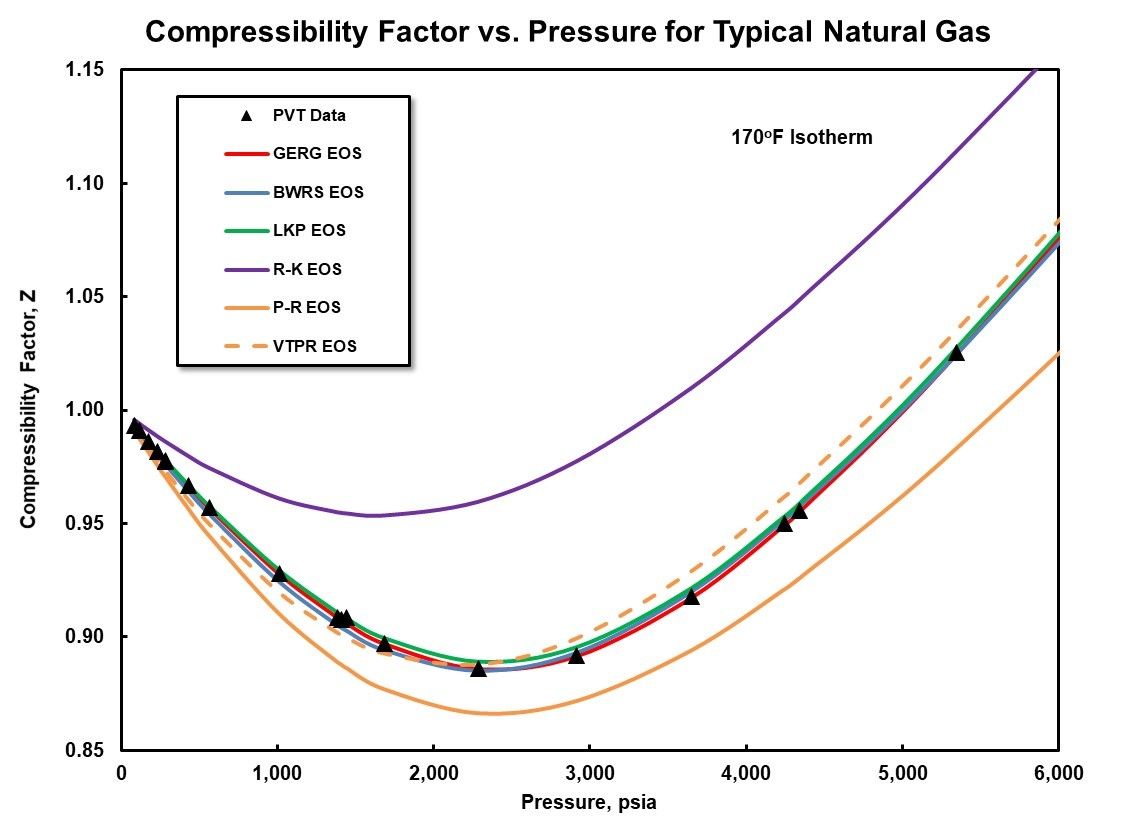
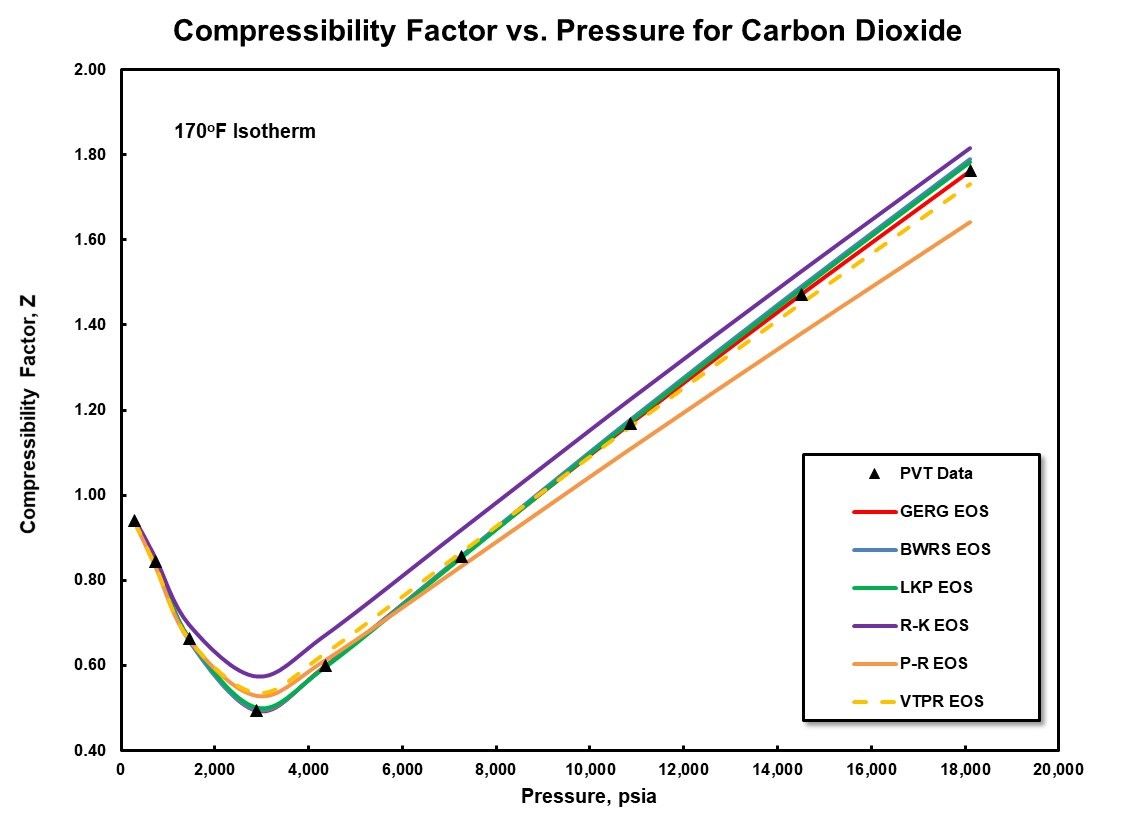
Figure 4: Equation of State Comparison for Carbon Dioxide.
EOS ACCURACY
The accuracy of any equation of state for a given single component gas or gas mixture can be validated by comparing its predicted compressibility factor (or specific volume) over a range of pressures and temperatures against laboratory measured values. There is a substantial amount of this laboratory generated PvT data available in the public technical literature. Usually, it is in the form of specific measured data points along isotherms across a range of pressures. This existing data may be utilized to verify the accuracy of a given equation of state proposed to evaluate a compressor application with the same or comparable single component gas or gas mixture. However, unique gas compositions may benefit from the generation of more specific experimental PvT data for the intended range of operating con-ditions. A number of laboratories exist that are capable of generating this data.
One example of an accuracy evaluation is provided in Figure 3 for a typical natural gas mixture. It is approximately 90% methane, 3% ethane, 1.5% propane, 1.7% carbon dioxide, and 1.7% nitrogen by volume. The experimental data was collected along a 170oF (76.7C) isotherm and a pressure range from atmospheric to 6000 psia (413.7 Bara). The experimental data points are provided as black triangles. Curves for the six different equations of state evaluated are included and designated in the legend.
The cubic equations of state display the largest deviations from the measured data. It should be noted that the volume-translated Peng-Robinson, VTPR EOS, shows improved agreement. The remaining equations of state demonstrate very good agreement with the experimental data. One final observation that should be highlighted is the good agreement with all equations of state. The exception is the R-K EOS at pressures below approximately 500 psia (34.5 Bara) along this isotherm. This is due to the behavior of this mixture at the lower pressures approaching those of an ideal gas at this relatively moderate temperature.
A second example is presented in Figure 4 for pure carbon dioxide across an increased pressure range up to a maximum of over 18,000 psia (1241 Bara). Good agreement is once again demonstrated for most of the equations of state evaluated with the largest deviations evident for the simpler, cubic equations of state.
These two figures are fairly representative for a large number of gas mixtures. But it is prudent to have a discussion between the equipment manufacturer and end user concerning the most appropriate equation of state to utilize for a specific application. As noted previously, if there is not ade-quate shared experience for unique gas mixtures, it may require the development of a program to empirically determine PvT data for the mixture and evaluation against a number of different equations of state to determine the most accurate.
The volumetric behavior of the gas is demonstrated through a comparison of PvT data and an equation of state. However, it is not obvious how this translates to other thermodynamic properties such as the internal energy, enthalpy and entropy. The perfect and ideal gas models described above state that these properties are related to the specific heats with the ideal gas model having the specific heats also being a function of the temperature. Experimental determination of specific heats is achieved through the use of a calorimeter, where an amount of energy is added to a thermally isolated gas sample and the increase in temperature is measured. A perfect gas would result in constant values of the measured specific heats over successive tests at different initial temperatures. But an ideal gas would reflect a temperature dependent value.
The real gas thermodynamic model is based upon the assumption that the specific heats are functions of both temperature and pressure. Although calorimeters exist that can measure specific heats at elevated pressures, most of this data has been derived from equipment that is designed to operate at relatively low pressures. Analyses of these real gas thermodynamic functions show that they can be expressed as the sum of the ideal gas value and an isothermal term that is a function of the pressure. This additive pressure dependent term is often referred to as the departure, or residual, function. Further mathematical evaluation can express these departure functions in terms of the compressibility factor which relates the value of the departure function to the value and accuracy of the compressibility factor. A few investigations into the accuracy of the departure functions as related to the predicted accuracy of the compress-ibility factor have confirmed this relationship. It is therefore plausible to assume that equation of state accuracy in the prediction of the compress-ibility factor can be extended to these additional thermodynamic parameters.
EQUATION OF STATE IMPACTS ON COMPRESSOR PERFORMANCE
It follows that equation of state differences in prediction of compressibility factor and the associated thermodynamic parameters may also influence the calculation of compressor thermodynamic performance parameters. These differences can readily be illustrated by comparing calculated polytropic work and efficiency for the various example equations of state based upon a common set of suction and discharge pressures and temperatures. Representative performance curves are first selected from actual applications with comparable gas compositions and suction conditions.
One of the evaluated equations of state is designated as the baseline and discharge pressures and temperatures are calculated for defined suction conditions at a number of points along the baseline performance curves. These sets of suction and discharge pres-sures and temperatures are then utilized to calculate polytropic work and efficiency for each of the equations of state. They are also used to plot performance curves, essentially in the same fashion as would occur in the case of acquired test data.
Baseline data included in the following comparisons was determined using the GERG EOS due to its demonstrated minimal deviation from published PvT data. Two examples are presented with both based upon the typical natural gas com-position defined previously. The first example addresses the comparative performance of a low-pressure case with a common suction pressure of 100 psia (6.89 Bara) and temperature of 100oF (37.8C). Discharge pres-sures range from approximately 208 psia (14.34 Bara) at higher inlet volumetric flows to 273 psia (18.82 Bara) at low flows near surge. Seven spe-cific operating points were evaluated and are presented in Figures 5 and 6. Polytropic work is plotted in Figure 5 versus an arbitrary range of inlet volumetric flow rates. Good agreement is displayed between the various equations of state.
Figure 5: Polytropic Work for Low Pressure Natural Gas.
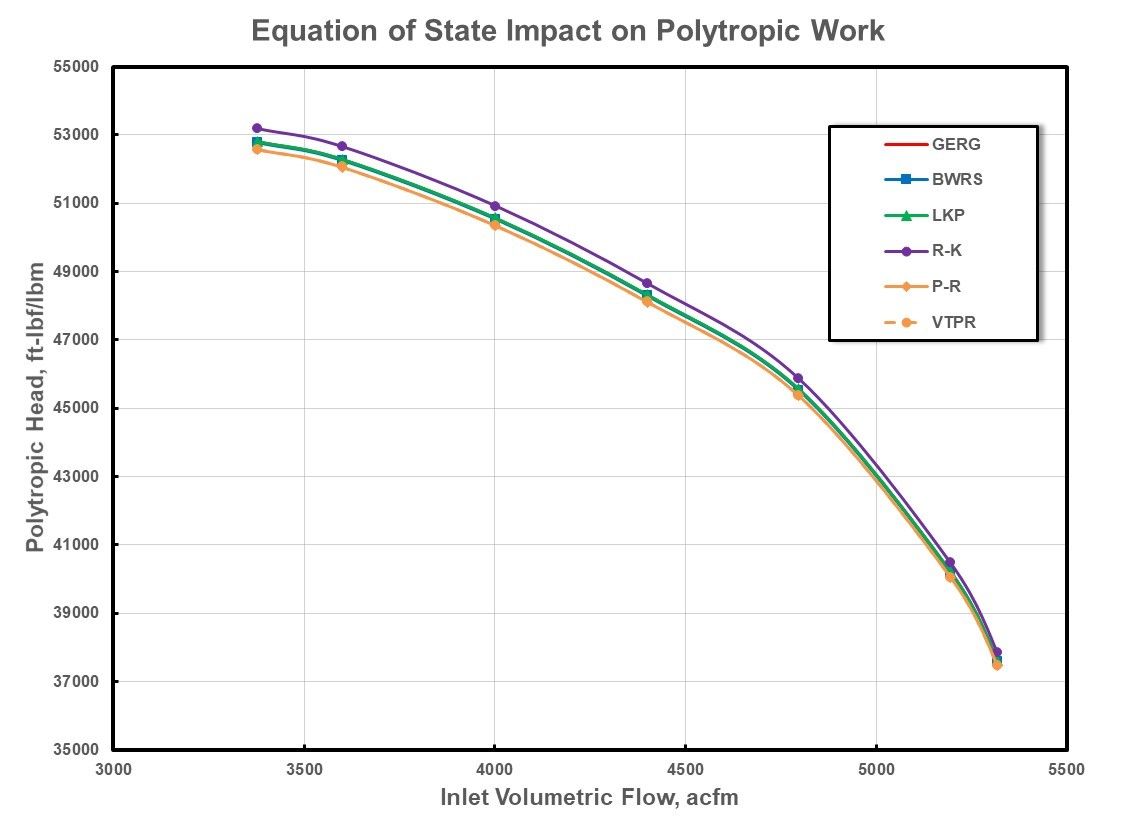
Figure 6: Polytropic Efficiency For Low Pressure Natural Gas.
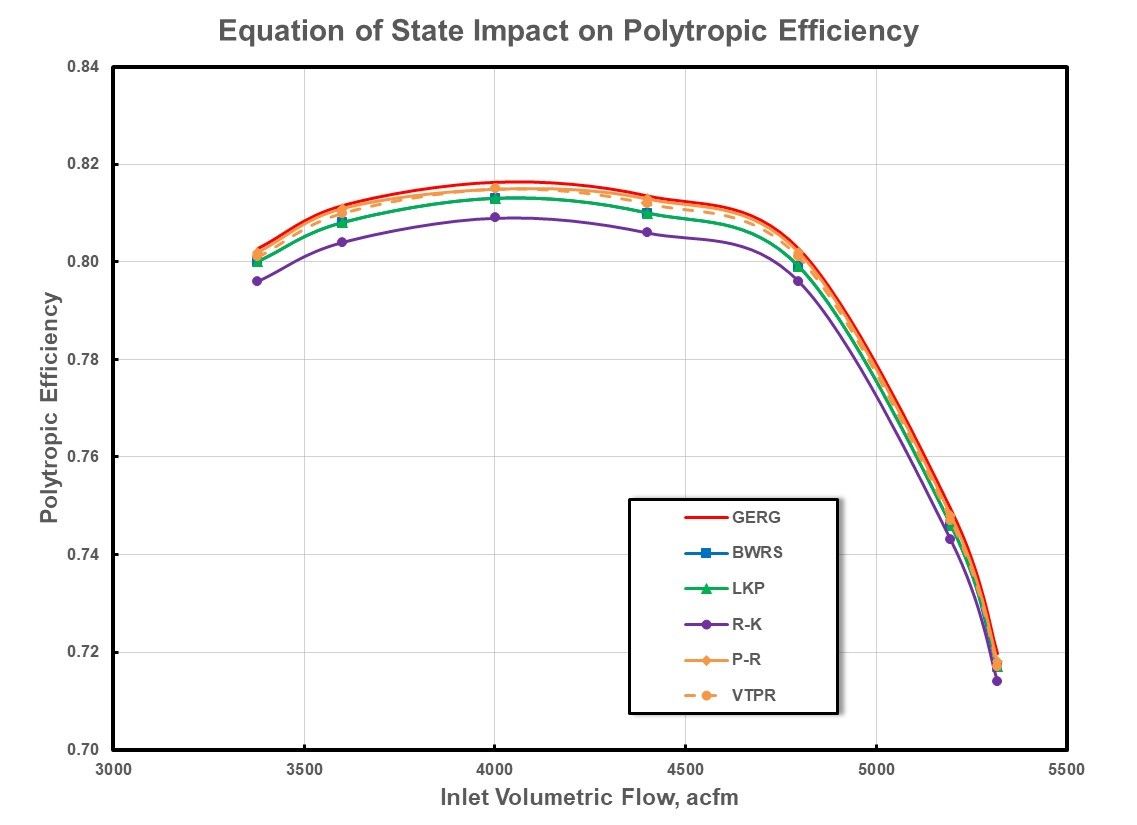
Although there appears to be more deviation in the polytropic efficiency than the polytropic work, a closer look at the scaling in Figure 6 also confirms good agreement between the different equations of state. These results could lead one to believe that there are insignificant differences based upon the choice of an equation of state. However, it should be recognized that there was little deviation in predicted compressibility factor in this range of pressures in Figure 3. Gas properties within this range of pressures and temperatures are near ideal with compressibility factor values near unity and with minimal differences between suction and discharge conditions between the equations of state.
As the pressure range of the compression application increases, differences in predicted compressibility factors become more evident. Using a similar procedure to predict discharge pressure and temperatures from defined suction conditions and a selected baseline polytropic work and efficiency curves, a comparison of calculated polytropic work and efficiency character-istics can be developed for the chosen set of equations of state.
Figure 7: Polytropic Work For High Pressure Natural Gas.
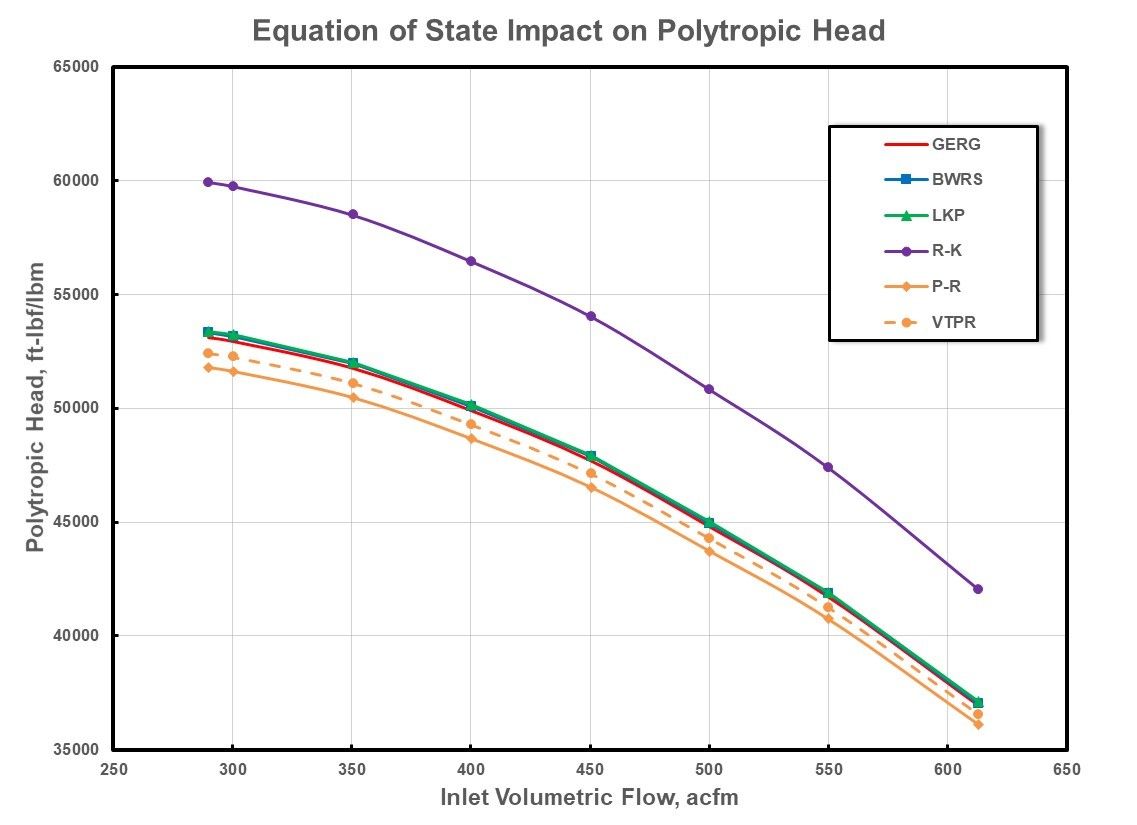
Figure 7 provides these curves using a common suction conditions of 2000 psia (137.9 Bara) and 100oF (37.8C) with discharge pressures ranging from 4349 psia (299.8 Bara) to 5553 psia (382.9 Bara) as determined with the GERG EOS.
Good agreement is evident among the more complex, virial type equations of state in comparison to obvious deviations with the cubic based equations of state. Significant deviations are noted for the R-K EOS across the entire inlet volumetric flow range, whereas the amount of deviation is decreased for the P-R EOS and minimized further for the VTPR EOS. This behavior lends credibility to the proposition that equation of state compressibility factor accuracy also translates to reduced uncertainty in the prediction of compressor performance.
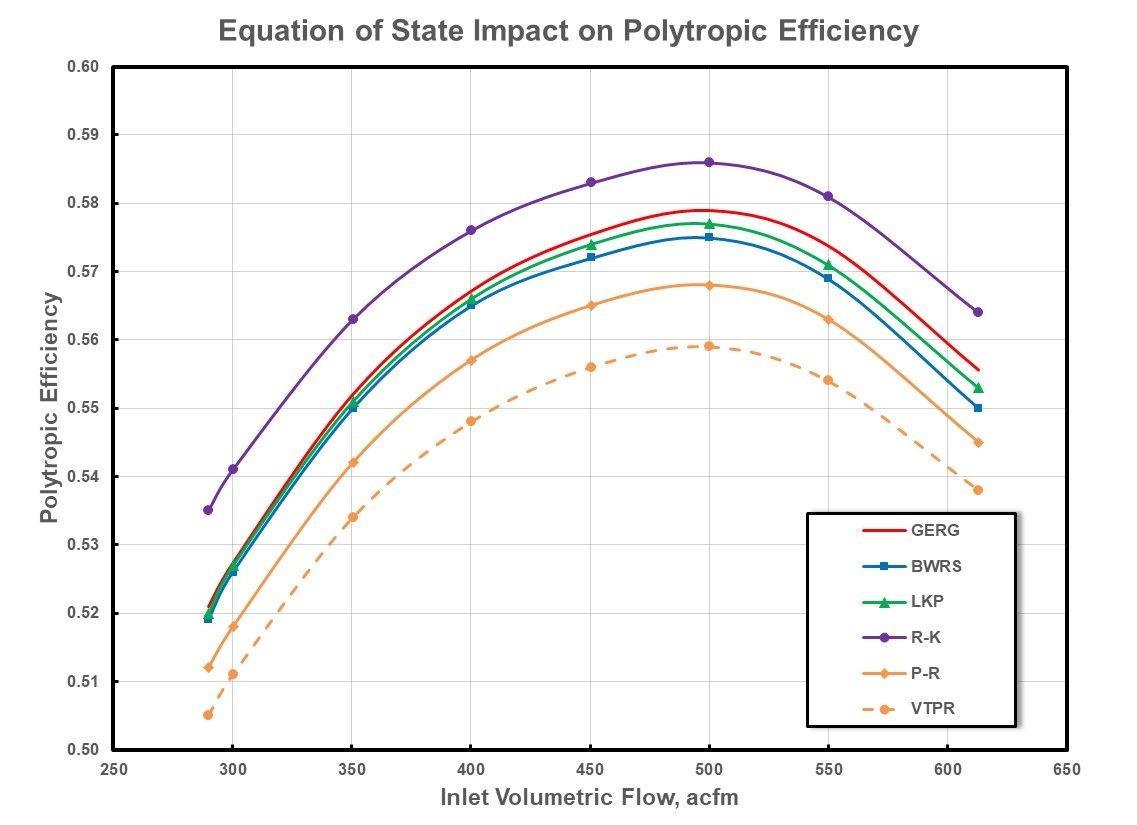
An equivalent evaluation of the polytropic efficiency is presented in Figure 8 for the higher-pressure case. Once again, greater deviation from the baseline is evident for the cubic equations of state. However, it is noted that the VTPR EOS displays greater deviation than the P-R EOS. This apparent shift in efficiency is due to the differences in the prediction of the enthalpy of the gas mixture at suction and discharge conditions, specifically the departure enthalpy term which is also a function of the compressibility factor. Recall that the efficiency is the ratio of the polytropic work to the enthalpy rise from suction to discharge conditions.
Figure 8: Polytropic Efficiency For High Pressure Natural Gas.
These examples demonstrate that the choice of equation of state used to estimate the thermodynamic properties can impact the calculation of recognized compressor performance parameters, particularly as gas conditions progressively depart from ideal gas behavior. A robust equation of state should adequately predict both ideal and real gas conditions. While these examples address a representative gas composition and set of operating conditions, the results may not apply to all potential applications. An evaluation of the most accurate equation of state for a specific application should be com-pleted to ensure the most accurate estimates of compressor performance parameters are obtained. It should be noted that the gas power required for the different equations of state at a common inlet volumetric flow rate shows less deviation across the wide range of conditions. This is due to a cancelation of compressibility factors between the polytropic head and flow rate relations, but does relate to a difference in mass flow rate for a common value of volumetric flow rate.
RECOMMENDATIONS
The information provided in this article leads to the following recommendations with respect to the application of a given equation of state in the evalu-ation of compressor thermodynamic performance.
1. Equipment supplier and user, or user’s representative, should discuss and agree upon the most appropriate equation of state for a specific application. This should be determined prior to equipment purchase commitment and utilized for both compressor and compression facility design activities.
2. If adequate information is not available to support the use of a specific equation of state, a program should be initiated to collect PvT data for the spe-cific gas/gas mixture across the anticipated pressure and temperature range of the application. This should be followed by an analysis of various equations of state to establish the most accurate.
3. Consistent use of a common equation of state should be utilized for initial compressor design and performance prediction, any planned ASME PTC 10 Type 1 (full pressure, similar gas composition) factory testing, field testing, and longer term operational compressor per-formance monitoring.
4. Given that factory ASME PTC 10 Type 2 testing is normally performed with inert gases at near ideal gas conditions, use of a common equation of state may not be necessary due to minimal deviations in thermodynamic properties.
◦Mark R. Sandberg, P.E. is the owner of Sandberg Turbomachinery Consulting. For more information, read the paper“A More Comprehensive Evaluation of Equation of State Influences on Compressor Performance Determination,” at https://oaktrust.library.tamu.edu/bitstream/handle/1969.1/166804.
